
![[pic of e and pi]](eandpi.gif)
Hi! We're E and Pi, here to introduce you to Jon Bettencourt's web page on unsolved math problems. It's his final project for COSMOS, the math and science program he's in. Is he going to be surprised when he sees what we've done!
Our favorite problem is the one about e(pi* n)
being close to integers, since it involves us! Although Pi says she likes the formula for any digit of pi better (of course).
n)
being close to integers, since it involves us! Although Pi says she likes the formula for any digit of pi better (of course).

To which Jon responds... I'm gonna get them for this! If E and Pi
keep messing with this page, I'll have to get Bromine to get them off my back, and I know they don't want that!
More information on E and Pi (the characters, not the numbers)
Anyway, I have been gathering information on unsolved problems from the Internet and other sources. Here are a few of the problems I have found and some information on some of them.
Some of these problems seem very simple, but end up with no simple proof or solution to them. As an example, Fermat's Last Theorem was very simple, but it took hundreds of years and some parts from very advanced branches of mathematics to solve it. So if one seems simple, don't try to solve it unless you know a lot of math.
More information about unsolved problems can be found with a search for unsolved problems on Google.com. Some of these are a little advanced, though; I only put the simpler ones up here.

Contents
Antipodes
The Collatz Conjecture
Coloring the Plane
Cube Triangulation
The Degree/Diameter Problem
e(pi*sqrt(n))
Folding a Napkin
A Formula for Any Digit of Pi
Goldbach's Conjecture
Maximum Matching
Odd Perfect Numbers
Perfect, Amicable, and Sociable Numbers
Perfect Rational Triangles
Poncelet's Theorem
Radical Differences
Repetition-Resistant Sequence
Smallest Possible Area
Tiling a Plane with Pentagons
Triangles and Tetrahedra
Twin Primes
My Problems
Sources Used

Antipodes
Jim Propp of the MIT Department of Mathematics proposes this problem:
Given a centrally symmetric convex compact body K in 3-space and a point p on its surface, the point on the surface farthest from p in the surface metric need not be the antipode of p. (Cf. the Knuth-Kotani puzzle, which asks one to find the point on the surface of a 1-by-1-by-2 box that is farthest from one of the corners; it is not the opposite corner.)
However, one might still conjecture that the maximum distance between two points in the surface metric, as both of them vary over the surface, is achieved by a pair of antipodal points. (This is believed to be true in the case of an a-by-b-by-c box for all a, b, and c, though to my knowledge no proof is known even for this very special case.)
Can anyone prove or disprove the conjecture? (Is the convexity condition necessary?)
Back to Contents

The Collatz Conjecture
Start with any positive integer. If it is even, divide it by 2, else multiply it by 3 and add 1. Continue. Will you always end up with the number 1?
If we start with 13, we will get the sequence:
13 40 20 10 5 16 8 4 2 1
So far, no counterexamples have been found. It has been verified that if you start with a number less than 700 billion, you will eventually end up with 1.
Back to Contents

Coloring the Plane
This is the famous Hadwiger-Nelson problem: How many colors are needed to color the points of the plane if no two points at unit distance receive the same color? The known results are:
- The graph can be 7-colored (try a hexagonal tessellation)
- There is a configuration that requires 4 colors
Thus, if 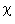 is the number of colors, then 4 <=
is the number of colors, then 4 <= 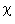 <= 7.
<= 7.
Back to Contents

Cube Triangulation
David Eppstein proposed this problem after responding to a question about splitting a cube into tetrahedra:This raises an interesting open question for higher dimensional hypercubes: what is the minimum number of simplices into which they can be cut? The long-diagonal construction generalizes to d! simplices in d dimensions, which can be reduced to O(d!/kd) for some k by using Cartesian products of the five-tetrahedron solution. There is also a lower bound of 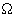 (
( (d!) kd) for another constant k coming from volume arguments (What is the largest simplex you can fit into a hypercube? This is equivalent to asking what's the largest determinant you can get with a 0-1 matrix, and is answered by the theory of Hadamard matrices.) Both bounds can be tightened slightly but there still remains a big gap between them. I'm not sure if it makes a difference whether you allow additional vertices or just stick with the original set of 2d vertices.
(d!) kd) for another constant k coming from volume arguments (What is the largest simplex you can fit into a hypercube? This is equivalent to asking what's the largest determinant you can get with a 0-1 matrix, and is answered by the theory of Hadamard matrices.) Both bounds can be tightened slightly but there still remains a big gap between them. I'm not sure if it makes a difference whether you allow additional vertices or just stick with the original set of 2d vertices.
I have here the original thread from which this problem comes from:
Click Here
Back to Contents

The Degree/Diameter Problem
No one has ever figured out a way to draw a graph whose size is greater than 12 (a graph with more than 12 vertices) that has all the following properties. Nor has anyone been able to figure out a good reason why it can't be done. A famous mathematician, Paul Erdos, has offered a large cash prize for the person who succeeds in drawing the graph that solves this problem.
Here are the properties the graph needs:- It is planar. Its edges can be drawn in a flat plane without crossing each other.
- The diameter is 3.
- It is 3-regular.
Back to Contents

e(pi* n)
n)
E: E and Pi here! Jon let us stay for a while and present this problem, since it's our favorite.
Pi: No, it's just your favorite problem, just because you're risen to some power in it. My favorite is the one about the digits of pi.
E: Yeah, yeah, yeah.
Some of the values of Exp(Pi* (n)) are very close to integers. A prize will be awarded to anyone who can either convincingly argue that this is coincidence, or who can explain why this is so in terms intelligible to an intelligent college senior. Something else that might help to lift the veil on this mystery would be a predictor: for a given value of n, is Exp(Pi*
(n)) are very close to integers. A prize will be awarded to anyone who can either convincingly argue that this is coincidence, or who can explain why this is so in terms intelligible to an intelligent college senior. Something else that might help to lift the veil on this mystery would be a predictor: for a given value of n, is Exp(Pi* (n)) close to an integer?
(n)) close to an integer?
Back to Contents

Folding a Napkin
Take a square napkin. Fold it (several times if you like) but keep it flat. Is it possible to get a shape with larger perimeter than the original one?
It is easy to show that one folding decreases the perimeter, but more folds may increase it again--can the perimeter ever be larger than it was from the start?
Back to Contents

A Formula for Any Digit of Pi
Pi: Pi here, to introduce my favorite problem. The formula for any digit of pi!
Jon: Pi, what are you doing here? I already let you introduce your... I mean, E's favorite problem. You said you would leave after that.
Pi: OK, OK! I'll go!
So far, the only ways of calculating a specific digit of Pi require calculations of all the previous digits.
However, a formula has been found that gives any hexadecimal (base 16) digit of pi without calculating all the previous digits! It was found by David Bailey, Peter Borwein, and Simon Plouffe. Here it is:
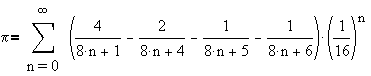
This is no longer an unsolved problem, but I put it up here because it is interesting that nobody even thought a digit-extraction formula for pi was possible, and now here it is.
Back to Contents

Goldbach's Conjecture
Can every even integer greater than 2 be written as the sum of two prime numbers? The conjecture is known to be true for all even integers less than 20 billion or so. It is also known that every "sufficiently large" even integer can be written as the sum of a prime number and an integer with at most two prime factors
Back to Contents

Maximum Matching
Andy Fingerhut proposes this problem:Given 6 arbitrary points in the euclidean plane, find a maximum matching for these 6 points. Let the matching be ((a1, b1), (a2, b2), (a3, b3)). Prove that there must exist a point x such that for all i, 1 <= i <= 3, dist(ai, x) + dist(x, bi) < 2/ (3) * dist(ai, bi) where dist(x, y) is the Euclidean distance between x and y.
(3) * dist(ai, bi) where dist(x, y) is the Euclidean distance between x and y.
One interesting consequence is that if such a point exists for any 6 points in the plane, then it also must exist for any even number of points in the plane.
Here's the original thread:
Click Here
Back to Contents

Odd Perfect Numbers
A perfect number is an integer that is equal to the sum of its factors, excluding itself. The first four perfect numbers are 6 (1+2+3), 28 (1+2+4+7+14), 496 (1+2+4+8+16+31+62+124+248), and 8128 (1+2+4+8+16+32+64+127+254+508+1016+2032+4064). The next one has eight digits.
So far, no odd perfect number has been found. However, it has been found that if there is an odd perfect number, it must be over 100 quindecillion (1050, or 1 followed by 50 zeros), cannot be of the form 2(n-1)*(2n-1) where (2n)-1 is prime, and must be the product of an odd prime and a perfect square.
Back to Contents

Perfect, Amicable, and Sociable Numbers
There is a whole other page about these, so I'll just point you to it:
Perfect, Amicable, and Sociable Numbers
Back to Contents

Perfect Rational Triangles
Does a perfect rational triangle exist? Question D21 in Richard K. Guy's book Unsolved Problems in Number Theory rudimentarily discusses the problem. This triangle is defined as one with rational sides, rationalmedians, rational altitudes, and rational area.
Here's the original thread:
Click Here
Back to Contents

Poncelet's Theorem
Let C1 and C2 be two circles in the plane, with C2 contained in C1. Pick a point A1 on C1. Draw line segment A1 A2 such that A2 is on C1 and A1 A2 is tangent to C2. Similarly, draw line segment A2 A3 such that A3 is on C1 and A2 A3 is tangent to C2. Continue for points A4, A5, etc., winding around C2.
Show that if the path returns to the original point after n points, i.e. An+1 = A1 for some n, then the path returns to the original point for any point A1 on C1.Furthermore, show that certain lines concur:
If n is even, say n = 2k, show that A1 Ak+1, A2 Ak+2, ..., Ak A2k concur.
If n is odd, say n = 2k + 1, let Ti be the point of tangency of C2 with Ai+k Ai+k+1 (the side "opposite" Ai, and taking subscripts modulo n), and show that A1 T1, A2 T2, ..., An Tn concur.
There is a proof of the first result using elliptic integrals - is there an easier proof?
Back to Contents

Radical Differences
Joseph O'Rourke presents this problem:
What is the minimum nonzero difference between two sums of square roots of integers? In particular, find a lower bound on r(n,k), the minimum positive value of: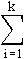
 (ai) -
(ai) - 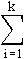
 (bi)
(bi)
where ai and bi are integers no larger than n.
Examples: r(20,2) =  (10)+
(10)+ (11)-
(11)- (5)-
(5)- (18) = approx .0002
(18) = approx .0002
r(20,3) =  (5)+
(5)+ (6)+
(6)+ (18)-
(18)- (4)-
(4)- (12)-
(12)- (12) = approx .000005
(12) = approx .000005
Back to Contents

Repetition-Resistant Sequence
R = (R(1), R(2), R(3), ...) = 1231132111212213121122211311133112321...
For each N, let L(N) be the longest length of the repeated string in the first N terms of R; e.g., L(19)=3, since within the first 19 terms, a string of length 3 (namely 121) repeats, and no longer string repeats.
You can write out many terms of R, using this rule: after the initial 123, at each stage, ask: when I append the next number (1, 2, or 3), will L(N + 1) increase, no matter which of the three I choose? If so, choose 1; otherwise, choose the least of the three for which L(N + 1) does not increase.
A finite string of 1's, 2's, and 3's is called a word. Here's the big question: does every word occur in R?
If so, then it is easy to see that every word repeats infinitely many times in R, which is notable, since the rule for generating R tries to resist repetition.
This problem has a reward of $50.
Back to Contents

Smallest Possible Area
A semi-circle with radius 1 can contain any curve of length 1 (if you're allowed to rotate and move the curve around). What is the area of the smallest (simply connected) set that can contain every curve of length 1?
Back to Contents

Tiling a Plane with Pentagons
There are some pentagons that will not tile a plane (the most famous one being the regular pentagon) and some pentagons that will tile a plane (the house shape, for example). Many ways of classifying pentagons that will or will not tile a plane have been created, but every time someone finds a pentagon that doesn't fit in with one of the classifications. There is no currently known way of classifying pentagons in this way.
Back to Contents

Triangles and Tetrahedra
Take a triangle ABC. A circle touches sides AB and AC and touches internally the circumcircle of ABC at A1. A circle touches the sides AB and AC and touches externally the circumcircle of ABC at A2. Similarly, define B1, B2, C1, C2. Let (X) denote the area of X. Prove that
(A1 B1 C1) <= (ABC) <= (A2 B2 C2).
Take a tetrahedron ABCD. A sphere touches the three faces containing A and touches internally the circumsphere of ABCD at A1. A circle touches the three faces containing A and touches externally the circumsphere of ABCD at A2. Similarly, define B1, B2, C1, C2, D1, D2. Let (X) denote the volume of X. Prove that
(A1 B1 C1 D1) <= (ABCD) <= (A2 B2 C2 D2).
Back to Contents

Twin Primes
Two consecutive prime numbers are called twin primes (e.g. 5 and 7, or 41 and 43, or 1,000,000,000,061 and 1,000,000,000,063 are twin primes). Is there an infinite number of twin primes?
Five and Seven: We're twins!!
Back to Contents

My Problems
These aren't exactly unsolved problems, but I'll put them up here just because I think they're interesting and maybe somebody will answer them.
Given any integer n, does n appear in an infinite decimal expansion of pi?
Given any integer n, does n appear in an infinite decimal expansion of e?
Given any integer n, does n appear in an infinite decimal expansion of  2?
2?
Given any integer n, does n appear in an infinite decimal expansion of (1+ 5)/2 (the golden ratio)?
5)/2 (the golden ratio)?
Given any integer n, does n appear in an infinite decimal expansion of sin(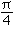 )?
)?
More generally, does any integer n appear in any irrational number?
Back to Contents

Sources Used
Pi: Hey! E and Pi here, one last time. We would just like to mention all the web sites that were used to create this page.
Jon: What are you two still doing here? I have nine digits of Bromine's phone number entered into my cell phone. If you don't go back to your algebra class, I'll dial the last one!
E and Pi: Uh oh.
Jon: Anyway, here are the sources I used.Internet Resources:
Ask Dr. Math
The Bailey-Borwein-Plouffe Pi Algorithm
The Exp(Pi*Sqrt(n)) Page
Games on Graphs
MathSoft Unsolved Problems
Open Problems for Undergraduates
Perfect, Amicable, and Sociable Numbers
sci.math (a discussion forum for mathematics)
Unsolved Problems
Unsolved Problems and Rewards
Unsolved Problems with Elementary Formulations
As mentioned before, more information about unsolved problems can be found with a search for unsolved problems on Google.com.
Miscellaneous Resources:
The paint can icon is © Microsoft Corporation.
E and Pi (and Bromine) are of my own creation.
Some of these problems were brought up during my classes here at COSMOS.
Back to Contents



![[pic of e and pi]](eandpi.gif)
 n)
being close to integers, since it involves us! Although Pi says she likes the formula for any digit of pi better (of course).
n)
being close to integers, since it involves us! Although Pi says she likes the formula for any digit of pi better (of course).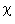 is the number of colors, then 4 <=
is the number of colors, then 4 <= 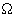 (
(
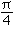 )?
)?